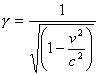Raum und Zeit |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Heute, fast 100 Jahre nach Einsteins erster Veröffentlichung der Relativitätstheorie, welche das Weltbild im letzten Jahrhundert doch so verändert und geprägt hat, ist diese vielen Menschen immer noch unbegreiflich und unverständlich. Hier wird versucht einen Einblick in die Theorie zu geben. Relativität vor dem 20. JahrhundertEs ist immer noch eine weit verbreitete Meinung, dass der bevorzugte Zustand eines Körpers die Ruhelage sei. Dies geht auf Aristoteles zurück, der behauptete: der natürliche Zustand eines Körpers sei die Ruhe. Newton schwächte diese Aussage ab. In seinem Werk „Principia Mathematica" formulierte Newton die Grundgesetze der Mechanik in konkreter mathematischer Sprache. Zwei der wichtigsten Aussagen (auch noch für uns) sind:1. Jeder Körper behält seinen Bewegungszustand bei, solange keine äußere Kraft auf ihn wirkt.Er übernahm bei seinen Überlegung auch das Prinzip der Galilei - Transformation(siehe Beispiel 1). Galilei hatte bereits herausgefunden, dass sich Geschwindigkeiten relativ verhalten. Der Begriff „Relativität", den Galilei prägte, ist der uns am einleuchtendste und geläufigste. Beispiel 1:Tom befindet sich in einem Zug, welcher mit 150 km/h fährt. Tom bewegt sich nun mit 6 km/h in Fahrtrichtung, also bewegt er sich relativ zum Zug mit 6 km/h. Für Bob, der an den Gleisen steht, bewegt der Zug sich mit 150 km/h und Tom im Zug mit 156 km/h. Zusammengefaßt:Man kann also die Geschwindigkeiten einfach addieren, um die relative Geschwindigkeit zwischen zwei Punkten zu errechnen. Weiterhin würde Tom sich in einem Zug befinden ohne Fenster, der konstant mit 150 km/h sich fortbewegt und weder beschleunigt noch abgebremst wird (wir vernachlässigen das hin und her schaukeln durch Scheinenunebenheiten oder Wind). So bewegt sich der Zug mit einer gleichmäßigen Bewegung und Tom wäre nicht in der Lage zu sagen, ob der Zug fährt oder nicht. Er kann also annehmen dass er ruht. Außerdem folgt daraus: Wenn Tom ruht, sich Bob mit 150 km/h von ihm weg bewegt, d.h. Bob bewegt sich und Tom ruht. Zusammengefaßt: Bobs Geschwindigkeit relativ zu Tom und dem Zug ist 150 km/h. Daraus folgt zusammen mit Newtons Gesetzen, dass es keinen absoluten Raum gibt. Man kann nicht sagen, dass zwei Ereignisse zu unterschiedlichen Zeitpunkten im selben Raum passiert sind, auch wenn der Ort im System identisch war. D. h. wenn Tom ein Buch auf seinem Sitzplatz liest und dabei zwischendurch auf Toilette geht, liest er zwar danach das Buch immer noch auf seinem Sitzplatz, aber relativ zum System außerhalb des Zuges nicht mehr im gleichen Raum. Ersetzen wir den Zug durch die Erde, so können wir die genaue Position auf der Erde bestimmen, aber nicht relativ gesehen zum gesamten Universum., d. h. der Raum ist nicht absolut festleg bar. Newton kannte dieses Problem, konnte aber einen nicht absoluten Raum mit seinem Weltbild nicht in Einklang bringen und vernachlässigte es daher. Die Tatsache, dass es keinen absoluten Raum gibt, ist von grundlegender Bedeutung für die Relativitätstheorie. Doch der entscheidende Versuch für die Relativitätstheorie mußte bis dahin noch gemacht werden. Nachdem O. Romer die Geschwindigkeit des Lichtes entdeckt hatte (mit Hilfe der Jupiter Monde), schaffte es der schottische Physiker James Clerk Maxwell die beiden Teiltheorien des Magnetismus und der Elektrizität in einer Theorie zu vereinigen. Er fand heraus, dass Licht sich wie eine elektromagnetische Welle verhält. Außerdem konnte er die Lichtgeschwindigkeit als Konstante in unserem System festlegen, dies ging aus seinen Formeln hervor. Ein amerikanischer Wissenschaftler (Michelson) wollte die Lichtgeschwindigkeit nun experimentell überprüfen. Das Michelson-Morley-Experiment führet zu folgender Beobachtung: das Licht besaß die gleiche Geschwindigkeit, ob man sich auf das Licht zu oder vor ihm weg bewegte. (Es war keine klassische Geschwindigkeitsaddition möglich.) Diese Beobachtung drohte die damalige Physik zu stürzen. Man konnte die Lichtgeschwindigkeit also nicht einfach addieren. Der niederländische Physiker Lorentz kam auf die Idee, dass das Licht, von welchem man damals vermutete, es würde sich durch einen Äther bewegen, seine eigene Zeit hätte. Er zweifelte jedoch nie an einer absoluten Zeit. Diese individuelle Zeit des Lichtes hätte das Phänomen erklären können. Es fehlte jedoch noch die passende Theorie, welche erst Einstein liefern konnte. Die Spezielle Relativitätstheorie (SRT)Am Anfang des 20. Jahrhundert war die Physik in ihren Grundfesten erschüttert. Es fehlt die Lösung zu einem Problem, welches erst in den letzten 40 Jahren entstanden war. Diese lieferte uns 1905 ein Patentbeamter aus Bern, Albert Einstein. Er betrachtete in seiner Überlegung zuerst nur das Licht und das Inertialsystem, d. h. ein System, in dem sich kräftefreie Körper befinden. Hier gilt das Trägheitsgesetz von Newton.Die gesamte Spezielle Relativitätstheorie besteht im Grunde auf zwei Postulaten, welche Einstein über die Natur des Universums gemacht hat. Das erste Postulat EinsteinsEs lautet so:
Dieses Prinzip ist ziemlich einfach und gehört zu unserm momentanem Weltverständnis. Wir denken meistens gar nicht daran, wenn wir es benutzen. Es ist selbstverständlich. An Hand eines Beispiels ist die schnell gezeigt: Beispiel 2:Wenn Tom im Zug das Papier von seinem Schokoladenriegel in den Mülleimer werfen will, braucht er sich keine Sorgen zu machen, dass sich dieser zu schnell bewegt. Der Zug fährt zwar mit 150 km/h , doch alle kräftefreien Körper, Tom, der Mülleimer und das Papier, befinden sich relative zum Zug in Ruhe. Tom macht sich daher zu recht keine Sorgen und kann ohne größere Probleme das Papier in den Mülleimer werfen. Für den Mülleimer stellt also der fahrende Zug ein Ruhesystem dar. Zu jedem kräftefreien Körper läßt sich solch ein System finden, in dem der Körper sich im Ruhezustand befindet. Auch hier kann man den Zug mit der Erde austauschen. Beim Fußball spielen macht sich Bob auch keine Sorgen darüber ob das Tor sich vielleicht wegbegebt, weil sich die Erde dreht.Die Beispiele zeigen, dass Einsteins Annahme über Inertialsysteme, welche entweder ruhen oder sich mit gleichbleibender gerader Geschwindigkeit bewegen, korrekt ist. Wir alle wissen, dass sozusagen Einstein der erste war, der dies so in Worte faßte. Einstein geht sogar noch weiter, er verbindet Raum und Zeit miteinander zur Raumzeit. Dies geht unmittelbar aus dem Verlust des absoluten Raumes und dem der absoluten Zeit, welcher durch die Relativitätstheorie begründet ist, hervor. Das zweite Postulat EinsteinsNachdem Maxwells Elektromagnetische Theorie mit den vier Gleichungen das Licht als elektromagnetische Welle enttarnt hatte und auch die Lichtgeschwindigkeit direkt aus seinen Gleichungen zu folgern war, konnte Einstein sein zweites Postulat aufstellen:
Das Zweite Postulat sagt im Prinzip aus, dass Maxwells Gleichungen in jedem
Inertialsystem gelten (vergleiche erstes Postulat). Diese Annahme führt jedoch zu einigen merkwürdigen Erscheinungen,
welche einer extra Erläuterung bedürfen. Diese treten allerdings erst
bei annähernder Lichtgeschwindigkeit auf. Beispiel 3:Diesmal sind Tom und Bob zwei Astronauten. Tom sitzt in seinem Hochgeschwindigkeitsraumschiff . Bob befindet befindet sich auf einem Außenposten. Das Raumschiff fliegt mit 100.000 km/s in Richtung Bob Außenposten. Tom will Bob eine Nachricht per Lichtsignal übermitteln. Wie schnell ist die Nachricht? Die Photonen des Lichtes bewegen sich mit ca. 300.000 km/s fort. Tom hat sie von seinem 100.000 km/h schnellen Raumschiff aus gesendet. Bob müßte also eine relative Geschwindigkeit des Lichtes von 400.000 km/s messen, wenn wir einfach die Geschwindigkeiten addieren würden wie in Beispiel 1. Halt, hier ist doch das selbe Problem, welches wir aus dem Michelson-Morley-Experiment kennen, oder? Dies würde Einsteins Aussage widersprechen, nach der Bobs Ergebnis mit Toms übereinstimmen müßte, also ca. 300.000 km/s entsprechen.Experimente haben gezeigt,dass Einsteins Postulate über die Lichtgeschwindigkeit stimmen und man die Geschwindigkeit nicht nach dem gleichem Prinzip addieren kann, wie gewohnt. Doch nun haben wir folgendes Problem: In unserem Beispiel hat sich nach einer Sekunde Tom relativ zu Bob mit 100.000 km bewegt. Das Licht hat relativ zu Tom 300.000 km zurückgelegt. Dann müßte das Licht also relativ zu Bob 400.000 km zurückgelegt haben. Es gibt dafür aber nur zwei Erklärungen: 1. Die 300.000 km, relativ zu Tom sind nicht wirklich 300.000 km im Vergleich zu Bob.Dieses Phänomen ist eines der merkwürdigsten Konsequenzen aus Einsteins zweitem Postulat. So erstaunlich es auch klingt, die Möglichkeiten der Erklärung sind beide tatsächlich korrekt. Exkurs : Der Gamma FaktorDieser Exkurs ist nicht nötig für das Verständnis der weiteren Punkte, allerdings ist er hilfreich bei der Verdeutlichung der relativistischen Effekte. Vorsicht: Er enthält Mathematik !!!!!!!!Um die Effekte der Relativitätstheorie ein bißchen anschaulicher zu
machen , führen wir einen Faktor ein, den Physiker als Gamma Faktor bezeichnen. Dieser hilft
relativistische
Effekte mathematisch zu beschreiben. Gamma hängt von der Geschwindigkeit des bewegten Objektes ab und bestimt Längen und Zeiten.
Wenn man sich die Formel genau anschaut, sieht man, warum wir im
alltäglichen Leben keine relativistischen Effekte wahrnehmen.
Aus der Tabelle geht deutlich hervor, dass selbst die Geschwindigkeit
einer Trägerrakete nicht ausreichen würde, um einen nennenswerten Effekt zu erzeugen. Gamma bleibt für
gewöhnliche Geschwindigkeiten so dicht bei 1, dass Länge und Zeit scheinbar unbeeinflußt
bleiben. Bei praktischen Anwendungen
treten relativistische Effekte erst in der Teilchenphysik auf, welche Elementarteilchen auf annähernde
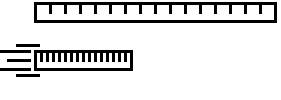
Lichtgeschwindigkeit beschleunigt. 1.LängenkontraktionDie Längenkontraktion beruht auf den von Lorentz schon vor Einstein entwickelten Formeln, welche das Michelson-Morley-Experiment erklären sollten. Aber erst Einstein konnte die nötig Theorie für diese Formeln und ihre komplette Bedeutung liefern. Er erklärt es durch die Spezielle Relativitätstheorie.Prinzipiell gilt dies: Die Länge eines Objektes in einem System, in dem es sich bewegt, ist kürzer als in einem System, indem es ruht (und zwar genau um den Faktor 1/γ. Eine klein Verdeutlichung anhand eines Lineals: ein ruhendes Lineal 2. ZeitdilatationDie Zeitdilatation, wirkt so:Die Zeit zwischen zwei Ereignissen, in einem System, in dem diese an unterschiedlichen Orten geschehen, ist länger als die Zeit zwischen den gleichen zwei Ereignissen in einem System, in dem sie am gleichen Ort geschehen. Dieser Effekt ist ein wenig komplizierter. Ein Beispiel hilft hier beim Verständnis. Beispiel 4:Eine Uhr bewegt sich sehr schnell von A nach B. Die Zeit, die sie braucht, wird einmal von ihr selbst bestimmt und das zweite Mal von einer ruhenden Uhr. Die ruhende Uhr mißt eine längere Zeit zwischen Verlassen des Punktes A und Ankunft am Punkt B. Die beiden Ereignisse finden für einen Beobachter bei der ruhenden Uhr an unterschiedlich Orten statt. Betrachtet man nun die andere Uhr und ihr Ruhesystem, so finden die beiden Ereignisse am gleichen Ort statt. Diese Uhr ruht auch, A und B bewegen(eine Folgen des Verlustes eines absoluten Raumes). Nach dem Satz mißt also die bewegte Uhr eine kürzer Zeit (die echte Zeit) und die ruhende nimmt eine längere Zeit wahr.Ein weiteres Beispiel. Beispiel 5:Angenommen ein Astronaut, mit einem Zwillingsbruder auf der Erde, reist während seiner fünfjährigen Mission mit fast 90% der Lichtgeschwindigkeit. So vergehen für seinen Zwillingsbruder auf der Erde zehn Jahr(5*γ). Der Astronaut lebt deshalb trotzdem nicht länger, er nimmt die Zeit nur anders wahr. Diese verhält sich relativ zueinander.Diese hypothetische Darstellung nennt man Zwillingsparadox. Entscheidend ist hier die Tatsache „gleichzeitig ist nicht gleichzeitig". Die Zeitdilatation ist Wirklichkeit. Sie wird in der
Elementarteilchenforschung genutzt, um Teilchen von
Nach diesen beiden Phänomenen gibt es noch mehr, eines der
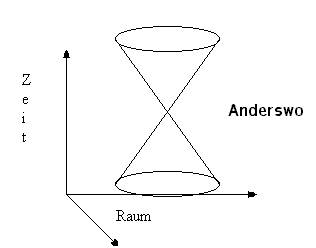
wichtigsten und wohl bekannteste betrifft die Energie eines Körpers. Wichtig hierbei ist die Äquivalenz von Energie und Masse. Die maximale GeschwindigkeitVielleicht ist euch aufgefallen, dass bis jetzt immer nur die Rede von annähernder Lichtgeschwindigkeit war, nie von Lichtgeschwindigkeit oder gar Überlichtgeschwindigkeit als Geschwindigkeit eines Raumschiffes oder Objektes die Rede war. Dies hat eine ganz simple physikalische Erklärung, welche direkt aus E=m*c2*γ folgt.Angenommen eine Rakete würde sich mit Lichtgeschwindigkeit fortbewegen, so würde γ für die Rakete gleich unendlich sein. Dies würde dann zwangsläufig die Konsequenz haben, dass man unendlich viel Energie aufgebracht hat, um die Rakete zu beschleunigen. Das ist definitiv nicht möglich. Daraus folgt, dass kein Körper, der eine Masse hat, je Lichtgeschwindigkeit erreichen wird. Aber auch Informationen können nicht mit Überlichtgeschwindigkeit übermittelt werden. Dies ist ebenfalls schnell deutlich gemacht. Wenn ein Fußball mit Überlichtgeschwindigkeit durch eine Scheibe geschossen würde, ging die Scheibe in manchen System kaputt, bevor der Fußball durch geflogen ist. Dies könnte dann den Zusammenhang zwischen Ursache und Wirkung durcheinander bringen und zu um logischen Konsequenzen führen. Besonders wenn der Ball, bevor er die Scheibe erreicht, aufgehalten wird. Die Lichtgeschwindigkeit ist eine unüberwindbare Barriere für uns, so lang die Relativitätstheorie gültig ist. Jedes Ereignis kann daher nur von einem bestimmten Informationskegel beeinflußt werden, dessen Mantel die Lichtgeschwindigkeit bildet. Selber kann das Ereignis nur Dinge beeinflussen, welche wiederum in einem Informationskegel liegen, den wieder die Lichtgeschwindigkeit in den maximalen Ausmaß bestimmt. Alles andere außerhalb der Kegel liegt im „Anderswo". Informationen aus dem Anderswo können das Ereignis erst in Zukunft erreichen. Ein typisches KegeldiagrammDer obere Teil stellt die Zukunft, der untere die Vergangenheit dar.
AllgemeinRelativitätstheorie (ART)Die Allgemeine Relativitätstheorie baut auf der Speziellen auf und wäre ohne diese nicht denkbar. Einstein veröffentlichte sie erst 1915, zehn Jahre nach der Speziellen Relativitätstheorie.Es ist wichtig, die beiden klassischen Definitionen von Masse zu kennen, um die Allgemeine Relativitätstheorie zu verstehen. 1. Es gibt einmal die "schwere" Masse, welche aus dem Gewicht eines Körpers folgt.Außerdem muß man verstehen, dass ein Gravitationsfeld eine konstante Beschleunigung erzeugt. Eine konstante Beschleunigung (in einem kleinen Raum) ähnelt also einem Gravitationsfeld. Das dritte Postulat EinsteinsDieses nennt man das Prinzip der Äquivalenz. Aufbauend auf der Gleichheit von schwerer und träger Masse sagt Einsteins drittes Postulat aus:
Beispiel 6:Nehmen wir einmal an, wir haben ein System X, welches eine gleichmäßig beschleunigte Bewegung relativ zu einem Inertialensystem K durchführt. Es befinden sich viele Objekte um K und X. Diese Objekte befinden sich in Ruhe relativ zu K. Daher werden diese Objekte relativ zu X gleichmäßig beschleunigt. Diese Beschleunigung ist für alle Objekte die gleiche und ist entgegengesetzt von der Beschleunigung von X relativ zu K. Aus der gleichen Beschleunigung für alle Objekte relativ zu X folgt als Effekt, dass X als in Ruhe angesehen werden kann und von einem Gravitationsfeld umgeben.Aus diesem Beispiel folgt, dass die schwere Masse eines Objekts im Gravitationsfeld identisch mit der trägen Masse des gleichen Objektes bei gleicher Beschleunigung ist. Das vierte Postulat EinsteinsDas vierte Postulat ist die Verallgemeinerung des Ersten. Es lautet:
Es kann nicht abgestritten werden das es natürlicher ist zu sagen, dass die Gesetze der Natur die gleichen sind in jedem System als nur in einem Inertialsystem. Dieses Prinzip heißt Prinzip der "Allgemeinen Relativität". Geometrie des UniversumsNatürlich sind Längenkontraktionen und Zeitdilatationen schon etwas sehr merkwürdiges, doch Einstein entdeckte noch eine andere sehr eigenartige Konsequenz seiner vier Postulate: Die Welt, in der wir leben, ist in den meisten nicht eine euklidische. Mit anderen Worten: parallele Linien können sich schneiden oder Kreise sind nicht rund und ein Dreieck kann drei 90º Winkel haben. Man kann also sagen, dass der Raum in unserem Universum gekrümmt ist. Die Gravitation ist dafür verantwortlich. Sie kann Raum und Zeit, also die Raumzeit, biegen, zerren, strecken und krümmen. Ein Beispiel verdeutlicht hier was gemeint ist. Beispiel 7 : Auch die Zeit wird gekrümmt durch das Gravitationfeld. Je stärker das Feld, desto länger dauert ein Sekunde relative zu einem schwacheren Feld. Dies lässt sich sogar beobachten. Ein Atomuhr auf einem hohen Berg läuft um Millionstel einer Sekunde schneller als eine Referenzuhr auf Meeresniveau. Es ist sehr wichtig für das Verständnis unserer Welt zu wissen, dass Raum und Zeit durch Gravitation gekrümmt werden können. Wir hoffen, dass wir die wichtigsten Aspekte der Relativitätstheorie gut verständlich und nicht zu lang darstellen konnten.
Autoren: Maximilian Gieseler und Marten Kuschert |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
© 2000 Physik LK 13 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||